応用情報技術者試験 令和6年春 午前問75 解説付き過去問
問題
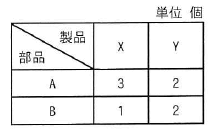
製品X、Yを1台製造するのに必要な部品数は、表のとおりである。
製品1台当たりの利益がX、Yともに1万円のとき、利益は最大何万円になるか。
ここで、部品Aは120個、部品Bは60個まで使えるものとする。

正解
解説
この問題は、限られた部品資源の下で製品XおよびYをどのような比率で生産すれば、最大の利益が得られるかを求める「線形計画法」に基づいた典型的な最適化問題である。
- 問題の整理
製品X・Yの1台あたりの部品使用数と、各部品の在庫は以下のとおりである。
- 製品X:部品Aを3個、部品Bを2個使用
- 製品Y:部品Aを1個、部品Bを2個使用
- 部品A:120個まで使用可能
- 部品B:60個まで使用可能
また、X・Yいずれも1台あたりの利益は1万円であるため、x台の製品Xとy台の製品Yを作ると、利益は (x + y) × 1万円 となる。 - 目的関数と制約条件の設定
目的:x + y の最大化(利益の最大化)
制約条件:
- 3x + 2y ≦ 120(部品Aの制約)
- x + 2y ≦ 60(部品Bの制約)
部品Bの制約は、両辺を2で割ると、x + y ≦ 30 となる。
したがって、以下の2つの制約を同時に満たす必要がある:
- 3x + 2y ≦ 120
- x + 2y ≦ 60 - 連立方程式による交点の求解
部品をすべて使い切るようなxとyの組合せ(制約式の境界線の交点)を求める。
- 3x + 2y = 120 …①
- x + 2y = 60 …②
① − ② を行うと:
(3x + 2y) − (x + 2y) = 120 − 60
→ 2x = 60
→ x = 30
この x = 30 を②に代入すると:
30 + 2y = 60
→ 2y = 30
→ y = 15 - 解の検証と最適解
x = 30、y = 15 のとき、部品Aの使用量は 3×30 + 2×15 = 90 + 30 = 120
部品Bの使用量は 1×30 + 2×15 = 30 + 30 = 60
どちらも制約内であり、資源をすべて使い切っているため、この組合せは最適解となる。
製品数:x + y = 30 + 15 = 45台
利益:45万円 - 補足:線形計画法の基本構造
この問題のように「制約条件」と「目的関数」が与えられ、それらを満たす中で目的関数を最大化(または最小化)する問題は、線形計画法(Linear Programming)として分類される。特に、xとyが整数かつ変数の数が2つである場合、グラフを用いた可視化や連立方程式による解析で容易に解を導くことができる。
