応用情報技術者試験 令和5年春 午前問75 解説付き過去問
問題
ビッグデータ分析の手法の一つであるデシジョンツリーを活用してマーケティング施策の判断に必要な事象を整理し、発生確率の精度を向上させた上で二つのマーケティング施策a、bの選択を行う。
マーケティング施策を実行した場合の利益増加額(売上増加額-費用)の期待値が最大となる施策と、そのときの利益増加額の期待値の組合せはどれか。
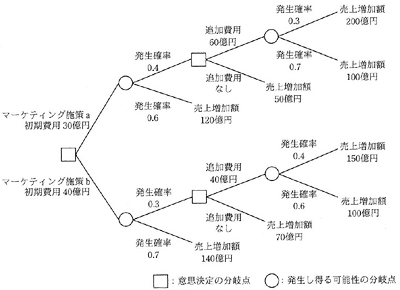

正解
解説
この問題は、デシジョンツリー(意思決定木)を用いて、二つのマーケティング施策a、bのうちどちらを選択すべきかを期待値に基づいて判断するものです。問題文中に追加費用の有無による分岐があるため、まず分岐点の期待値を評価し、その後全体の期待値を求める必要があります。
- 施策aの分岐点の期待値を計算
施策aの中で、発生確率0.4の分岐では追加費用の有無で期待値が変わります。
・追加費用あり:200×0.3+100×0.7-60=60+70-60=70億円
・追加費用なし:50億円
→ 期待値が高い「追加費用あり」を選択(70億円) - 施策bの分岐点の期待値を計算
施策bの中で、発生確率0.3の分岐も同様に検討します。
・追加費用あり:150×0.4+100×0.6-40=60+60-40=80億円
・追加費用なし:70億円
→ 期待値が高い「追加費用あり」を選択(80億円) - 施策aの全体の期待値を計算
施策aの成功時(確率0.6)は利益120億円、失敗時(確率0.4)は上記で求めた70億円、初期費用が30億円。
期待値=120×0.6+70×0.4-30=72+28-30=70億円 - 施策bの全体の期待値を計算
施策bの成功時(確率0.7)は利益140億円、失敗時(確率0.3)は上記で求めた80億円、初期費用が40億円。
期待値=140×0.7+80×0.3-40=98+24-40=82億円
したがって、期待値が最大となる施策はbであり、そのときの利益増加額の期待値は82億円となります。
