応用情報技術者試験 令和5年春 午前問21 解説付き過去問
問題
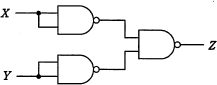
NAND素子を用いた次の組合せ回路の出力Zを表す式はどれか。
ここで、論理式中の"・"は論理積、"+"は論理和、
"X"はXの否定を表す。

正解
解説
この問題は、NANDゲートだけで構成された論理回路の出力Zについて、その論理式を導き出す問題です。NANDゲートの基本動作とド・モルガンの法則を使って回路の動作を分析します。
- NANDゲートの性質
NANDゲートは「ANDの否定」を出力する論理回路であり、入力XとYに対して次の出力をします:
X NAND Y = X・Y - 構成回路の解析
問題の回路は以下の3つのNANDゲートで構成されています。
- 最初のNANDゲート:XとXを入力 → X・X = X
- 次のNANDゲート:YとYを入力 → Y・Y = Y
- 最後のNANDゲート:上記2つの出力(X と Y)を入力 → X・Y
X・Y = X+Y - 最初のNANDゲート:XとXを入力 → X・X = X
- 真理値表による確認
入力XとYにすべての組合せ(00, 01, 10, 11)を与えて出力Zを確認すると、ZはX+Yと一致します。したがって、この回路はORゲートと等価です。
以上より、このNAND素子で構成された回路の出力Zを表す式は X+Y です。
