応用情報技術者試験 令和6年秋 午前問72 解説付き過去問
問題
製造業のA社では、NC工作機械を用いて、四つの仕事a~dを行っている。
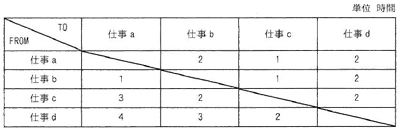
各仕事間の段取り時間は表のとおりである。
合計の段取り時間が最小になるように仕事を行った場合の合計段取り時間は何時間か。
ここで、仕事はどの順序で行ってもよく、a~dを一度ずつ行うものとし、FROMからTOへの段取り時間で算出する。

正解
解説
NC工作機械で複数の仕事を行う場合、仕事の順序によって段取り時間の合計が変化する。そこで、合計段取り時間が最小となる順序を求める必要がある。
- 段取り時間の考え方
段取り時間とは、ある仕事から次の仕事へ移行する際にかかる時間であり、全ての仕事を一度ずつ行う際に最小の合計段取り時間を求めるには、最適な順序を見つける必要がある。 - 最適な順序の求め方
すべての組み合わせ(24通り)を試すことも可能だが、段取り時間が1時間のものを優先すると効率的である。
段取り時間が1時間の「a→c」「b→a」「b→c」を優先して利用すると、b→a(1時間)とa→c(1時間)の順序を使って、b→a→cが2時間で構成できる。
残る仕事dは、仕事cの後に配置することで、2時間の段取り時間となる。 - 計算結果
最適な順序は b→a→c→d であり、合計段取り時間は以下の通り:
1時間(b→a) + 1時間(a→c) + 2時間(c→d) = 4時間 となる。
このように、NC工作機械の段取り時間を考慮することで、生産効率を向上させることが可能となる。
