応用情報技術者試験 令和4年秋 午前問52 解説付き過去問
問題
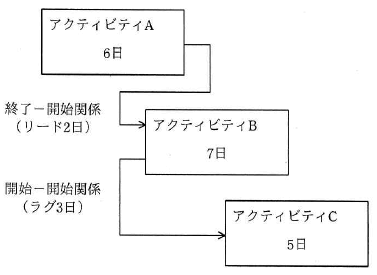
図は、実施する三つのアクティビティについて、プレシデンスダイアグラム法を用いて、依存関係及び必要な作業日数を示したものである。
全ての作業を完了するための所要日数は最少で何日か。

正解
解説
この問題は、プロジェクト管理におけるプレシデンスダイアグラム法(PDM)を用いて、タスク間の依存関係やリード・ラグを考慮しながら、全体の所要日数を最小で求める能力を問うものです。
- プレシデンスダイアグラム法の概要
プレシデンスダイアグラム法は、作業(アクティビティ)をノード(四角)で表し、それらの依存関係を矢印で示す図法です。アクティビティ間の関係には、次の4種類があります。
・終了-開始(FS)
・開始-開始(SS)
・終了-終了(FF)
・開始-終了(SF)
また、作業開始・終了の前倒しや遅延を表す「リード」や「ラグ」も設定できます。 - アクティビティの関係の把握
問題の図には3つのアクティビティ(A、B、C)が示されています。それぞれの関係は以下のとおりです。
・アクティビティA → B:FS(終了-開始)+リード2日 → Aが終了する2日前にBを開始できる
・アクティビティB → C:SS(開始-開始)+ラグ3日 → Bが開始してから3日後にCを開始できる - 最少所要日数の計算
作業日数はそれぞれ、A=5日、B=6日、C=4日とします。
・Aは0日目に開始し、5日目に終了
・BはA終了の2日前(3日目)に開始し、6日間かかるので8日目に終了
・CはB開始から3日後(6日目)に開始し、4日間かかるので9日目に終了
したがって、すべての作業が完了するのは9日目でCが終了したときですが、開始日は0日目とするため、必要な所要日数は「12日間」となります。
以上より、リードやラグを考慮した上でスケジュールを調整すると、全体の所要日数は最少で12日であると判断できます。
