応用情報技術者試験令和3年春午前問14 解説付き過去問

問題

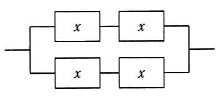
稼働率がxである装置を四つ組み合わせて、図のようなシステムを作ったときの稼働率をf(x)とする。区間 0≦x≦1 におけるy=f(x)の傾向を表すグラフはどれか。ここで、破線はy=xのグラフである。

この問題は、複数の装置を組み合わせたシステムの稼働率を求める問題です。稼働率がxである装置を四つ組み合わせた場合のシステムの稼働率f(x)に関して、グラフの傾向を選ぶ問題となります。

装置の稼働率の計算
装置が四つ組み合わさっているため、システムが停止する確率は、一つでも故障している場合に相当します。装置一つが故障する確率は X = 1 - x です。したがって、四つの装置が全て故障している確率は X⁴ = (1 - x)⁴ と表されます。システムが動作する確率、即ち稼働率f(x)は、1 - (1 - x)⁴ で求めることができます。
グラフの特性
計算式から、xが0から1に向かうにつれて、f(x)は0から1へと増加することがわかります。また、x = 0のときf(x) = 0、x = 1のときf(x) = 1となるため、y = xという線から始まり、上に凸の形状をしていることが予測されます。さらに、xが小さい値の時、(1 - x)⁴は急速に1に近づくため、f(x)の増加は非常に早くなります。これにより、グラフはxの小さい領域で急激に増加し、徐々に増加率が緩やかになる形をとります。

したがって、この特性をもっともよく表しているのは、選択肢の中で唯一上に凸の形状を示しているグラフが正解です。