応用情報技術者試験 令和2年秋 午前問47 解説付き過去問
問題
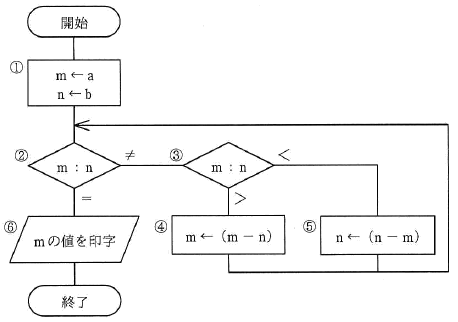
次の流れ図において、①→②→③→⑤→②→③→④→②→⑥ の順に実行させるために、①においてmとnに与えるべき初期値aとbの関係はどれか。
ここで、a,bはともに正の整数とする。

正解
解説
この問題は、流れ図に従って処理が進み、指定された順「①→②→③→⑤→②→③→④→②→⑥」で処理が終了するように、初期値として与える m(a)と n(b)の関係を求める問題です。
- 流れ図の処理の基本
最初に①で m ← a、n ← b の代入が行われ、以後は条件分岐によって処理が進みます。②~④、⑤は m と n の大小比較により分岐し、n ← n-m または m ← m-n の処理を行います。最終的に m=n となったとき、処理が終了します(⑥に到達)。 - 処理順から逆算して関係を求める
問題では「①→②→③→⑤→②→③→④→②→⑥」の順に進むような a, b を求めます。これは以下のような処理順です。
・最初の②→③→⑤より、初期状態では m<n(a<b)
・次の②→③→④より、更新後の状態では m>n
・その後、②→⑥に進むため、m=n になる必要がある
処理⑤では「n ← n-m」、次の④では「m ← m-n」です。
④の処理後に m=n となっていることから、④の処理直前の m は m ← m-n によって更新される前なので、「更新後のm」と「n」の和、すなわち m=n の関係から「更新前のm」は 2n だったことがわかります。
その一つ前の⑤では「n ← n-m」。ここでの m は 2n だったので、更新前の n は m+n=3n です。したがって初期値として m=2n、n=3n に対応する比率となります。
この関係から初期値 a, b において a:b=2:3 であればよいとわかります。 - 数式での確認
a:b=2:3 を式にすると、3a=2b となります。
この関係が正しい初期値の条件です。
したがって、初期値として与える m(a)と n(b)の関係は「3a=2b」が正しい答えです。
