応用情報技術者試験 令和元年秋 午前問54 解説付き過去問
問題
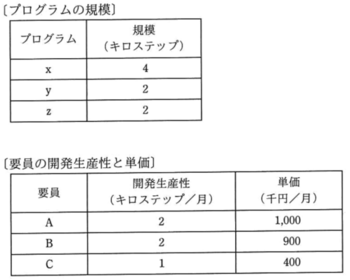
プログラムx,y,zの開発を2か月以内に完了したい。
外部から調達可能な要員はA,B,Cの3名であり、開発生産性と単価が異なる。
このプログラム群を開発する最小のコストは、何千円か。
ここで、各プログラムの開発は、それぞれ1名が担当し、要員は開発生産性どおりの効率で開発できるものとする。
また、それぞれの要員は、担当したプログラムの開発が完了する時点までの契約とする。

正解
解説
この問題は、異なる開発生産性と単価を持つ3人の要員を、3つのプログラム(x, y, z)に割り当て、2か月以内に完了させる条件で、最小の開発コストを求めるものです。
- 各要員の生産性とコスト
要員A:月に2キロステップ、生産単価 1,000千円
要員B:月に2キロステップ、生産単価 900千円
要員C:月に1キロステップ、生産単価 400千円
1キロステップ当たりのコストで比較すると、最も安価なのはC(400)、次にB(450)、A(500)となります。 - プログラムx(4キロステップ)の割当
プログラムxは2か月以内に完成させる必要があり、1か月に2キロステップ以上の生産性が必要です。要員Cは月1キロステップのためxは担当不可。AまたはBで対応可能ですが、コストが安いB(900×2か月=1,800千円)に担当させるのが最適です。 - プログラムy(2キロステップ)とz(2キロステップ)の割当
残るAとCを、yとzに割り当てます。Cは2か月契約で2キロステップ開発可能(400×2=800千円)
Aは1か月で2キロステップ開発可能(1,000×1=1,000千円)
この2人で残りのプログラムを2か月以内に対応可能です。
以上より、要員の割当とコストは以下の通りです:
B(x担当):900×2=1,800千円
C(y担当):400×2=800千円
A(z担当):1,000×1=1,000千円
合計:3,600千円
したがって、最小の開発コストは3,600千円です。
