応用情報技術者試験 令和元年秋 午前問52 解説付き過去問
問題
アローダイアグラムで表される作業A~Hを見直したところ、作業Dだけが短縮可能であり、その所要日数は6日間に短縮できることが分かった。
作業全体の所要日数は何日間短縮できるか。
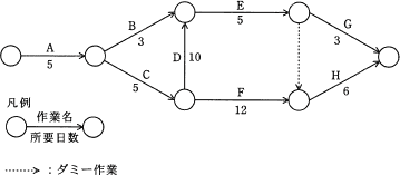

正解
解説
この問題は、アローダイアグラムにおけるクリティカルパスを把握し、作業Dの短縮がプロジェクト全体の所要日数に与える影響を正しく評価できるかを問うものです。
- 現状のクリティカルパスの特定
まず、各経路の所要日数を計算し、最も長い経路(クリティカルパス)を求めます。クリティカルパスは、プロジェクトの完了までの最短期間を決定するため、ここでの判断が重要です。
与えられた図から、作業Dの所要日数が10日間の状態では、「A→C→D→E→(ダミー)→H」の経路が最長の31日間となり、これがクリティカルパスであることがわかります。 - 作業Dの短縮による影響
作業Dを6日間に短縮すると、クリティカルパス上の合計日数は 31-4=27日間になります。これにより、「A→C→F→H」(28日間)の経路が新たなクリティカルパスになります。
このとき、プロジェクト全体の最短所要日数は28日間となるため、作業Dの短縮により、プロジェクト全体で3日間の短縮が可能です。 - 他の経路の確認
他のパス(例えばA→B→E→G や A→B→E→H)は、短縮前後ともに所要日数が28日未満であり、短縮後のクリティカルパスにはなりません。
したがって、作業Dを6日間に短縮することで、プロジェクト全体の所要日数は3日間短縮されます。
