応用情報技術者試験 平成31年春 午前問23 解説付き過去問
問題
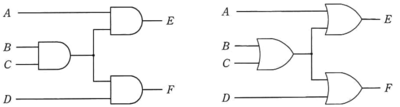
次の二つの回路の入力に値を与えたとき、表の入力A,B,C,Dと出力E,Fの組合せのうち、全ての素子が論理積素子で構成された左側の回路でだけ成立するものはどれか。

正解
解説
- 左側の回路の構造(全て論理積)
左側の回路はすべて論理積(AND)素子で構成されている。構造は以下の通り:
・BとCをAND → 中間出力
・中間出力とAをAND → 出力E
・中間出力とDをAND → 出力F - 右側の回路の構造(全て論理和)
右側の回路は論理和(OR)素子で構成されている。構造は以下の通り:
・BとCをOR → 中間出力
・中間出力とAをOR → 出力E
・中間出力とDをOR → 出力F
-
入力 A=0, B=0, C=0, D=0
出力 E=0, F=0
- 左回路(論理積)
B(0)・C(0)=0
A(0)・(B・C)(0)=0
→E=0
(B・C)(0)・D(0)=0
→F=0
⇒成立 - 左回路(論理積)
B(0)+C(0)=0
A(0)+(B+C)(0)=0
→E=0
(B+C)(0)+D(0)=0
→F=0
⇒成立
- 左回路(論理積)
-
入力 A=0, B=0, C=1, D=1
出力 E=1, F=1
- 左回路(論理積)
B(0)・C(1)=0
A(0)・(B・C)(0)=0
→E=0
(B・C)(0)・D(1)=0
→F=0
⇒不成立 - 左回路(論理和)
B(0)+C(1)=1
A(0)+(B+C)(1)=1
→E=1
(B+C)(1)+D(1)=1
→F=1
⇒成立
- 左回路(論理積)
-
入力 A=1, B=1, C=0, D=1
出力 E=0, F=0
- 左回路(論理積)
B(1)・C(0)=0
A(1)・(B・C)(0)=0
→E=0
(B・C)(0)・D(1)=0
→F=0
⇒成立 - 左回路(論理和)
B(1)+C(0)=1
A(1)+(B+C)(1)=1
→E=1
(B+C)(1)+D(1)=1
→F=1
⇒不成立
- 左回路(論理積)
-
入力 A=1, B=1, C=1, D=1
出力 E=1, F=1
- 左回路(論理積)
B(1)・C(1)=1
A(1)・(B・C)(1)=1
→E=1
(B・C)(1)・D(1)=1
→F=1
⇒成立 - 左回路(論理和)
B(1)+C(1)=1
A(1)+(B+C)(1)=1
→E=1
(B+C)(1)+D(1)=1
→F=1
⇒成立
- 左回路(論理積)
