応用情報技術者試験 令和7年春 午前問13 解説付き過去問
問題
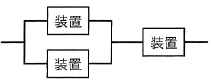
図のように3個の装置を並列と直列に組み合わせて構成したシステムがある。
装置単体の稼働率と、システムの稼働率の関係を示したグラフはどれか。
ここで、3個の装置の稼働率は、全て等しいものとする。

正解
解説
この問題は、複数の装置を直列および並列に組み合わせたシステムにおいて、装置単体の稼働率とシステム全体の稼働率の関係を問うものです。
- システム構成の理解
図に示されたシステムは、2つの装置を並列に配置し、それに直列で1つの装置を接続した構成です。並列構成では、いずれか1台が稼働していれば全体として稼働するとみなされ、直列構成ではすべての装置が稼働していなければならないという特性があります。 - 稼働率の計算
各装置の稼働率を r としたとき、まず並列に配置された2装置の稼働率は次のように求められます。
2台とも停止する確率は (1 − r)² なので、並列部分の稼働率は 1 − (1 − r)² = 2r − r² です。
これに直列で装置1台(稼働率 r)を接続するため、システム全体の稼働率は (2r − r²) × r = 2r² − r³ となります。 - グラフの形状の考察
関数 2r² − r³ は、原点を通り、単調増加しながら最終的に1へと近づく非線形の曲線です。この関数は、r が0に近いときには非常に低く、r が高まるにつれて急激にシステム稼働率が向上する特性を持ちます。
このような性質は、直線 y = r と比較すると下に位置しながらも後半で急上昇する形状、すなわち「上に凸な曲線」として表されます。これに該当するのは、右肩上がりの曲線で中央付近にやや緩やかな傾きがあるグラフです。
したがって、装置単体の稼働率とシステム全体の稼働率の関係を示す正しいグラフは、装置の稼働率が向上するにつれて加速度的にシステム稼働率が上昇する特性を持つ曲線です。
