応用情報技術者試験 令和6年春 午前問5 解説付き過去問
問題
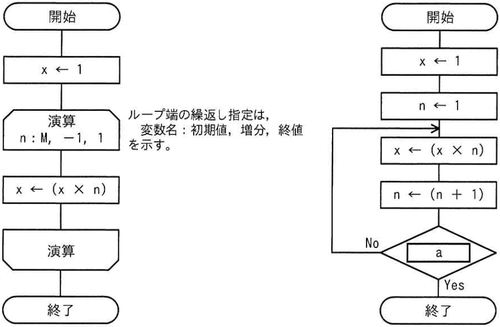
正の整数Mに対して、次の二つの流れ図に示すアルゴリズムを実行したとき、結果xの値が等しくなるようにしたい。
aに入れる条件として、適切なものはどれか。

正解
解説
正の整数Mに対して、二つの流れ図のアルゴリズムを実行したときに結果Xが等しくなるような条件aを求める。
二つの流れ図の動作を以下で詳しく示す。
二つの流れ図の動作を以下で詳しく示す。
- 左側の流れ図の動作
左側の流れ図は、次のような動作をする。
- 初期値として X = 1 を設定する。
- n を M から始め、1 になるまで1ずつ減らしながら繰り返し処理を行う。
- 繰り返しの中で X に n を掛ける。
- 繰り返しが終了すると、その時点の X の値を結果として出力する。
- n = 3 の場合:X = 1 × 3 = 3
- n = 2 の場合:X = 3 × 2 = 6
- n = 1 の場合:X = 6 × 1 = 6
- ループ終了後の結果:X = 6
つまり、左側の流れ図の最終結果は M の階乗(M!)となる。 - 初期値として X = 1 を設定する。
- 右側の流れ図の動作
右側の流れ図は、次のような動作をする。
- 初期値として X = 1、n = 1 を設定する。
- n が条件aを超えるまで、1ずつ増やしながら繰り返し処理を行う。
- 繰り返しの中で X に n を掛ける。
- 繰り返しが終了すると、その時点の X の値を結果として出力する。
- n = 1 の場合:X = 1 × 1 = 1、次に n は2になる
- n = 2 の場合:X = 1 × 2 = 2、次に n は3になる
- n = 3 の場合:X = 2 × 3 = 6、次に n は4になる
- n = 4 で条件aを満たし、ループ終了すると結果は X = 6 となる。
つまり、右側の流れ図の結果が M! になるのは、条件aが M より大きいとき(n > M)である。 - 初期値として X = 1、n = 1 を設定する。
- 両方の流れ図が一致する条件
左側の流れ図は常に M! を出力するため、右側の流れ図も M! となる必要がある。
右側の流れ図が M! になるためには、条件aは n > M である必要がある。
したがって、適切な条件は「n > M」となる。
