応用情報技術者試験令和2年秋午前問23 解説付き過去問

問題

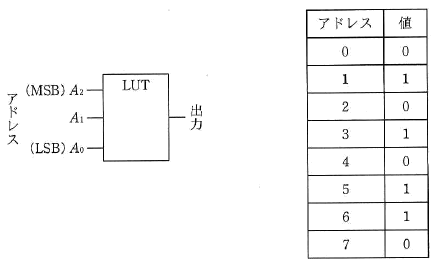
次の表に示す値が格納されたLUT(Lookup Table)と等価な回路はどれか。ここで、LUTのアドレス信号A₂～A₀はA₀がLSBで、各回路の入力信号aがA₂,bがA₁,cがA₀に対応する。

この問題は、3ビットの入力（a, b, c）に対して出力値が定義されたLUT（Lookup Table）の内容と等価な論理回路を識別する問題です。各ビットの対応は a＝A₂、b＝A₁、c＝A₀（LSB）とされています。

LUTの出力条件の整理
与えられた表から、アドレス（入力の組合せ）と出力値は次のようになっています：
000 → 0
001 → 1
010 → 0
011 → 1
100 → 0
101 → 1
110 → 1
111 → 0
このうち、出力が1となるアドレスは以下の4つです。
・001（a＝0, b＝0, c＝1）
・011（a＝0, b＝1, c＝1）
・101（a＝1, b＝0, c＝1）
・110（a＝1, b＝1, c＝0）
論理式の導出
出力が1となる入力条件を論理積で表すと次のようになります：
・a・b・c
・a・b・c
・a・b・c
・a・b・c
これらを論理和でまとめると、以下の積和形論理式になります：
Y ＝ a・b・c ＋ a・b・c ＋ a・b・c ＋ a・b・c
等価な回路の判定
この論理式を具現化した回路を選択肢から確認すると、各項をANDゲートで構成し、それらをORゲートでまとめた回路が該当します。これにより、LUTに記録されたすべての1の出力条件に対して正しく1を出力し、それ以外では0を出力します。

以上により、このLUTと等価な論理動作をするのは、上記の論理式を満たす回路です。