応用情報技術者試験 平成30年春 午前問5 解説付き過去問
問題
非負の整数m、nに対して次のとおりに定義された関数 Ack(m、n) がある。
Ack(1,3) の値はどれか。
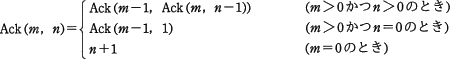
Ack(1,3) の値はどれか。
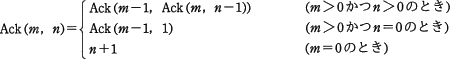
正解
解説
この問題は、アッカーマン関数 Ack(m, n) の定義に従って、Ack(1, 3) の値を再帰的に計算する問題です。アッカーマン関数は計算の過程が複雑になるため、定義に忠実に展開していくことが重要です。
- アッカーマン関数の定義
アッカーマン関数は、以下のように定義されます:
・Ack(0, n) = n + 1
・Ack(m, 0) = Ack(m - 1, 1) (m > 0)
・Ack(m, n) = Ack(m - 1, Ack(m, n - 1)) (m > 0 かつ n > 0) - Ack(1, 3) の計算
定義に従って、Ack(1, 3) を順に展開します:
Ack(1, 3) = Ack(0, Ack(1, 2))
Ack(1, 2) = Ack(0, Ack(1, 1))
Ack(1, 1) = Ack(0, Ack(1, 0))
Ack(1, 0) = Ack(0, 1) = 2
Ack(1, 1) = Ack(0, 2) = 3
Ack(1, 2) = Ack(0, 3) = 4
Ack(1, 3) = Ack(0, 4) = 5
したがって、Ack(1, 3) の最終的な値は 5 となります。
この問題では、関数の定義に沿って丁寧に再帰を展開し、1つずつ確実に計算を進めていくことが正解を導く鍵です。
